Hodrick–Prescott filter
The Hodrick–Prescott filter is a mathematical tool used in macroeconomics, especially in real business cycle theory to separate the cyclical component of a time series from raw data. It is used to obtain a smoothed-curve representation of a time series, one that is more sensitive to long-term than to short-term fluctuations. The adjustment of the sensitivity of the trend to short-term fluctuations is achieved by modifying a multiplier  . The filter was first applied by economists Robert J. Hodrick and Nobel Prize(2004) winner Edward C. Prescott.[1] Though Hodrick and Prescott popularized the filter in the field of economics, it was first proposed by E. T. Whittaker (Whittaker, E. T. (1923). On a new method of graduation, Proceedings of the Edinburgh Mathematical Association, 78, 81-89.)[2]
. The filter was first applied by economists Robert J. Hodrick and Nobel Prize(2004) winner Edward C. Prescott.[1] Though Hodrick and Prescott popularized the filter in the field of economics, it was first proposed by E. T. Whittaker (Whittaker, E. T. (1923). On a new method of graduation, Proceedings of the Edinburgh Mathematical Association, 78, 81-89.)[2]
Contents |
The equation
The reasoning for the methodology uses ideas related to the decomposition of time series. Let 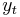 for
for 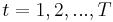 denote the logarithms of a time series variable. The series
denote the logarithms of a time series variable. The series 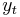 is made up of a trend component, denoted by
is made up of a trend component, denoted by 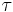 and a cyclical component, denoted by
and a cyclical component, denoted by 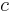 such that
such that 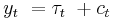 .[3] Given an adequately chosen, positive value of
.[3] Given an adequately chosen, positive value of  , there is a trend component that will minimize
, there is a trend component that will minimize
- min
![\sum_{t = 1}^T {(y_t - \tau _t )^2 } %2B \lambda \sum_{t = 2}^{T - 1} {[(\tau _{t%2B1} - \tau _t) - (\tau _t - \tau _{t - 1} )]^2 }.\,](/2012-wikipedia_en_all_nopic_01_2012/I/302de546828ebee8262fe6ea95501bcc.png)
The first term of the equation is the sum of the squared deviations 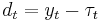 which penalizes the cyclical component. The second term is a multiple
which penalizes the cyclical component. The second term is a multiple  of the sum of the squares of the trend component's second differences. This second term penalizes variations in the growth rate of the trend component. The larger the value of
of the sum of the squares of the trend component's second differences. This second term penalizes variations in the growth rate of the trend component. The larger the value of  , the higher is the penalty. Hodrick and Prescott advise that, for quarterly data, a value of
, the higher is the penalty. Hodrick and Prescott advise that, for quarterly data, a value of 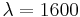 is reasonable.[4]
is reasonable.[4]
Drawbacks to the H–P filter
The Hodrick–Prescott filter will only be optimal when:[5]
- Data exists in a I(2) trend.
- If one-time permanent shocks or split growth rates occur, the filter will generate shifts in the trend that do not actually exist.
- Noise in data is approximately normally distributed.
- Analysis is purely historical and static (closed domain). The filter has misleading predictive outcome when used dynamically since the algorithm changes (during iteration for minimization) the past state (unlike a moving average) of the time series to adjust for the current state regardless of the size of
 used.
used.
See also
References
- ^ Hodrick, Robert, and Edward C. Prescott (1997), "Postwar U.S. Business Cycles: An Empirical Investigation," Journal of Money, Credit, and Banking, 29 (1), 1–16.
- ^ http://cowles.econ.yale.edu/P/cd/d17b/d1771.pdf
- ^ Kim, Hyeongwoo. "Hodrick–Prescott Filter" March 12, 2004
- ^ Ravn, Morten; Uhlig, Harald (2002). "On adjusting the Hodrick–Prescott filter for the frequency of observations". The Review of Economics and Statistics 84 (2): 371–375.
- ^ French, Mark. "Estimating changes in trend growth of total factor productivity: Kalman and H–P filters versus a Markov-switching framework" September 6th, 2001